Minimax

Minimax 算法常用于「有限状态，零和，完全信息（，两人）」博弈问题，比如棋类

问题定义

输入

• 可能的状态 state，$s \in S$（棋盘的局面）
• 允许的动作 action，$a \in A(s)$（即可以落子的位置）
• A transition model，$T(s, a) \colon S \times A \to S$（比如黑白棋的翻转，围棋的提子）
• 效用函数 utility function，$u(s,p)$，即玩家 $p$ 在游戏结束时（状态 $s$）获得的「收益」

其中前三者决定了 game tree（博弈树），也即搜索空间

A branch of a game tree. (source: 5D Chess With Multiverse Time Travel)

输出

• 策略 strategy，$\pi(s) \colon S \to A$，即在给定状态（棋局）下选择一个动作（落子）

Minimax 算法

在零和博弈的设定下，玩家一的目标为最大化自己的收益 $\max u_1$，玩家二的目标则等价于最小化玩家一的收益 $\min u_1$，方便起见分别称为玩家 Max 和 Min。给定一个 game tree，最优策略可以由每个节点的 minimax 值决定

• Minimax 值，一个递归定义的值，表示从当前状态 $s$ 开始，双方均采取最优策略直至游戏结束时玩家一 (Max) 的效用值

  $$\text{minimax}(s) = \begin{cases} u(s, \texttt{Max}) & \text{if GameOver}(s) \\ \max_{a \in A(s)} \text{minimax}(s^\prime) & \text{if }\texttt{Max}\text{'s turn} \\ \min_{a \in A(s)}\text{minimax}(s^\prime) & \text{if }\texttt{Min}\text{'s turn} \\ \end{cases}$$

  其中 $s^\prime=T(s,a)$

从上述定义中不难看出，计算 minimax 值时需要沿着 game tree 一直推演（深度优先）至叶子节点（游戏结束），然后回溯计算出之前每个节点的值。一个节点只要计算出了 minimax 值，就已经看到了游戏的结局（效用值）──假如对手 (Min) 也采取最优策略的话。如果 Min 不采取最优策略，Max 仍然采取 minimax 策略，Max 的最终效用只会更高（不一定最优）。

然后算出了 minimax 值

假设 game tree 的深度为 $m$，每个节点有 $b$ 种走法，则该算法的时间复杂度为 $O(b^m)$，在实际情况中是不现实的。

Python 代码

## https://github.com/aimacode/aima-python/blob/master/games.py

def minmax_decision(state, game):
    """Given a state in a game, calculate the best move by searching
    forward all the way to the terminal states. [Figure 5.3]"""

    player = game.to_move(state)

    def max_value(state):
        if game.terminal_test(state):
            return game.utility(state, player)
        v = -np.inf
        for a in game.actions(state):
            v = max(v, min_value(game.result(state, a)))
        return v

    def min_value(state):
        if game.terminal_test(state):
            return game.utility(state, player)
        v = np.inf
        for a in game.actions(state):
            v = min(v, max_value(game.result(state, a)))
        return v

    # Body of minmax_decision:
    return max(game.actions(state), key=lambda a: min_value(game.result(state, a)))

Alpha-Beta 剪枝

假设我们当前处于 $s$ 节点，并且已经计算出了其一个直接子节点 $m$ 的 minimax 值，那么对于 $s$ 的其它后代节点，如果 $n$「差于」$m$，那么 $n$ 节点肯定不是最优路线了

Alpha-beta 剪枝原理

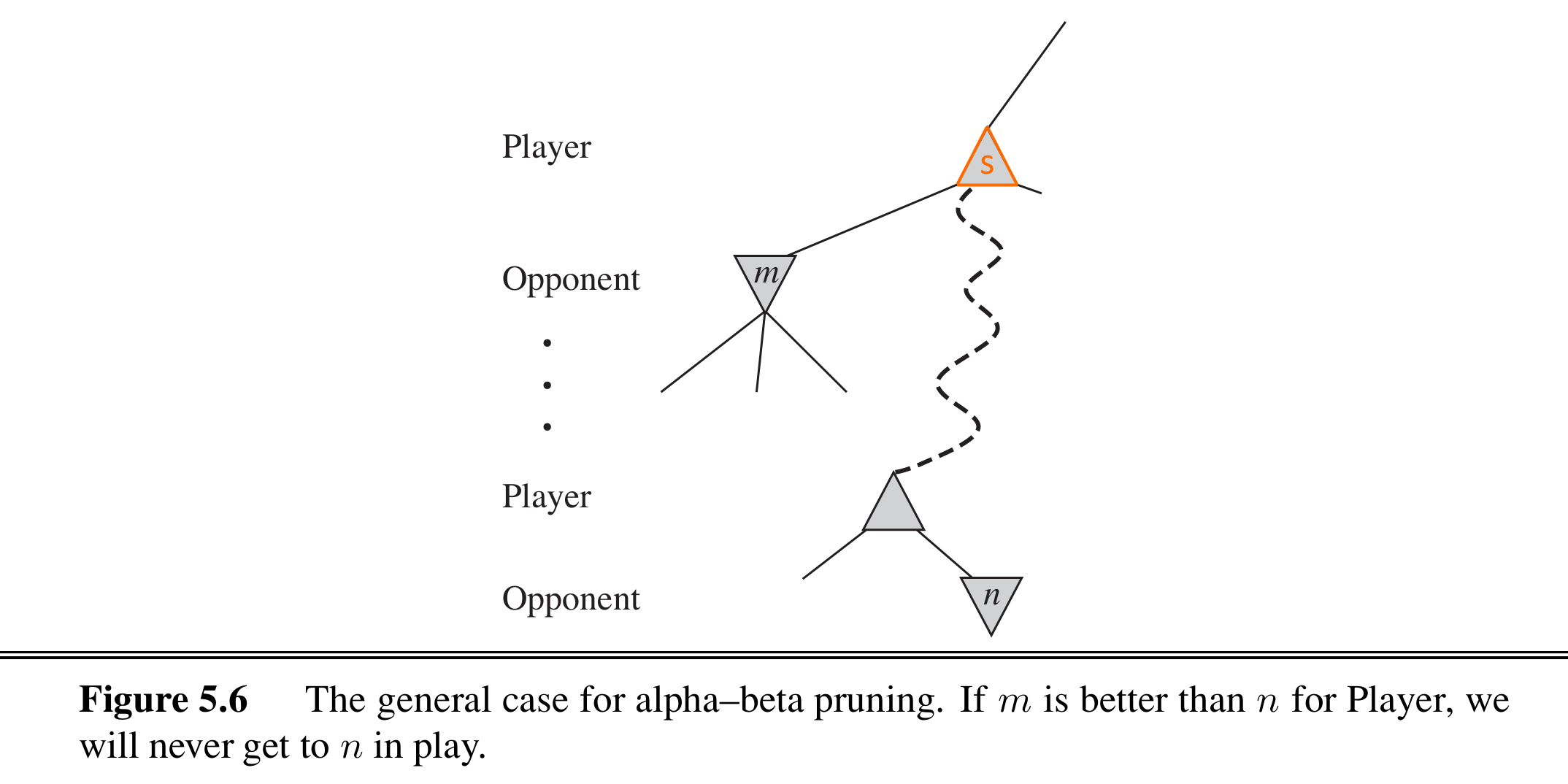
具体来说，对于一个 Max 节点（例如 $s$），每计算出一个子节点 $m_i$ 都会更新 $s$ 的下限（$s \ge \alpha$），其中 $\alpha=\text{max}(m_1,m_2,\dots)$。在 $s$ 还未探索的后代节点中，如果发现某个节点 $n\le\alpha$，也就表明其肯定不是最优解，其后续分支也可以剪掉（即无需再考察 $n$ 的其它子节点）。而想要确定 $n\le\alpha$，需要两个条件：① $n$ 是 Min 节点，② $n$ 的一个子节点 $n^\prime\le\alpha$。
（简而言之，在 Max 节点中更新已知最小效益 $\alpha$，在其后代的 Min 节点中发现小于 $\alpha$ 的效益时剪枝，即直接 return）

同理，假如 $s$ 是 Min 节点，已知的子节点会确定 $s$ 的上限（$s \le \beta$），$\beta=\text{min}(m_1,m_2,\dots)$。剪枝只会发生在其后代的某个 Max 节点 $n$，如果发现 $(n\ge)\,n^\prime\ge\beta$。

每个节点的 $\alpha$，$\beta$ 值继承于它的父节点。

A step-by-step example

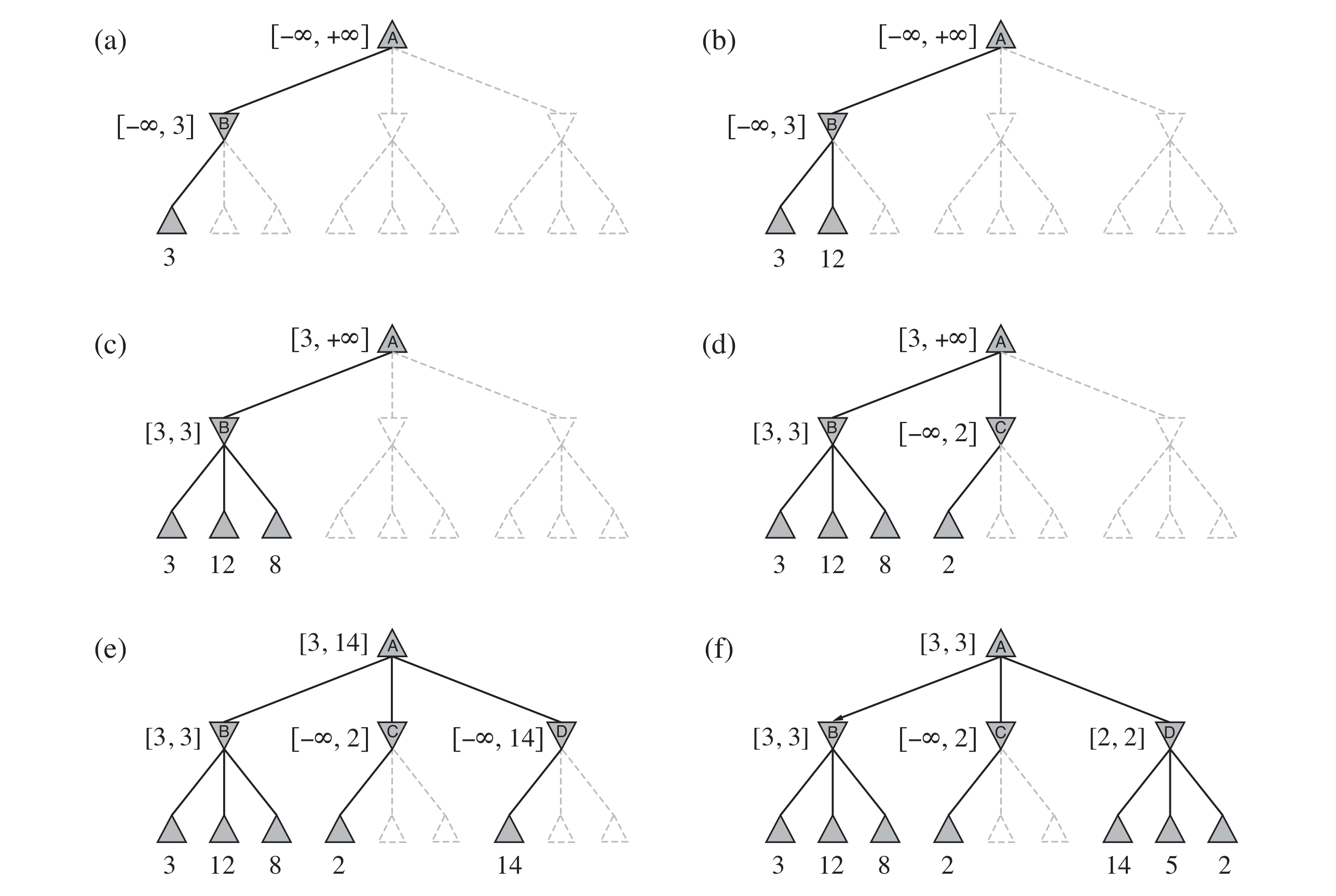
Python 代码

## https://github.com/aimacode/aima-python/blob/master/games.py

def alpha_beta_search(state, game):
    """Search game to determine best action; use alpha-beta pruning.
    As in [Figure 5.7], this version searches all the way to the leaves."""

    player = game.to_move(state)

    # Functions used by alpha_beta
    def max_value(state, alpha, beta):
        if game.terminal_test(state):
            return game.utility(state, player)
        v = -np.inf
        for a in game.actions(state):
            v = max(v, min_value(game.result(state, a), alpha, beta))
            if v >= beta:
                return v
            alpha = max(alpha, v)
        return v

    def min_value(state, alpha, beta):
        if game.terminal_test(state):
            return game.utility(state, player)
        v = np.inf
        for a in game.actions(state):
            v = min(v, max_value(game.result(state, a), alpha, beta))
            if v <= alpha:
                return v
            beta = min(beta, v)
        return v

    # Body of alpha_beta_search:
    best_score = -np.inf
    beta = np.inf
    best_action = None
    for a in game.actions(state):
        v = min_value(game.result(state, a), best_score, beta)
        if v > best_score:
            best_score = v
            best_action = a
    return best_action

TIP

即使使用了 alpha-beta 剪枝，在实际中也基本不可能搜索到游戏结束，这就需要使用启发式评估函数 (heuristic evaluation function) 来代替游戏结束时的效用函数，这里不再展开。

其它

在搜索资料的时候偶然发现 LeetCode 上也有一些 minimax 相关的题目 (opens new window)，比如

486. 预测赢家 (opens new window)

给定一个表示分数的非负整数数组。 玩家一从数组任意一端拿取一个分数，随后玩家二继续从剩余数组任意一端拿取分数，然后玩家一拿，…… 。每次一个玩家只能拿取一个分数，分数被拿取之后不再可取。直到没有剩余分数可取时游戏结束。最终获得分数总和最多的玩家获胜。

给定一个表示分数的数组，预测玩家一是否会成为赢家（包括平局）。你可以假设每个玩家的玩法都会使他的分数最大化。

示例：

输入：[1, 5, 2]
输出：False

输入：[1, 5, 233, 7]
输出：True

最朴素 minimax 解法

class Solution:
    def PredictTheWinner(self, nums: List[int]) -> bool:

        l = len(nums)
        if l == 1:
            return True

        def max_value(i, j, hist_sum):
            if i == j:
                return hist_sum + nums[i]
            v_i = min_value(i + 1, j, hist_sum + nums[i])
            v_j = min_value(i, j - 1, hist_sum + nums[j])
            return max(v_i, v_j)

        def min_value(i, j, hist_sum):
            if i == j:
                return hist_sum
            v_i = max_value(i + 1, j, hist_sum)
            v_j = max_value(i, j - 1, hist_sum)
            return min(v_i, v_j)

        v_0 = min_value(1, l - 1, nums[0])
        v__1 = min_value(0, l - 2, nums[l - 1])
        return max(v_0, v__1) >= sum(nums) / 2

然后一运行，，直接倒数

执行用时: 5012 ms (beats 13.11% of python3 submissions)
内存消耗: 14.1 MB

假如依据题目特性提前剪枝（max_value 和 min_value 函数中）

if hist_sum >= half_sum:  ## sum(nums) / 2
    return hist_sum

执行用时: 4280 ms (beats 22.67% of python3 submissions)
内存消耗: 13.6 MB

好了一丢丢，但是还是不太行

那么既然有递归（和很多重复计算的可能性），加一点缓存如何？（注意缓存和剪枝有冲突，因为剪枝往往会依赖一些额外的 context，比如 hist_sum，alpha/beta，而缓存一般不会记录这些）

minimax + 缓存

class Solution:
    def PredictTheWinner(self, nums: List[int]) -> bool:
        l = len(nums)
        if l == 1:
            return True

        cache = {}

        def max_value(i, j, hist_sum):
            if i == j:
                return hist_sum + nums[i]
            if f"{i}-{j}" in cache.keys():
                return cache.get(f"{i}-{j}") + hist_sum
            v_i = min_value(i + 1, j, hist_sum + nums[i])
            v_j = min_value(i, j - 1, hist_sum + nums[j])
            v = max(v_i, v_j)
            cache.update({f"{i}-{j}": v - hist_sum})
            return v

        def min_value(i, j, hist_sum):
            if i == j:
                return hist_sum
            if f"{i}-{j}" in cache.keys():
                return cache.get(f"{i}-{j}") + hist_sum
            v_i = max_value(i + 1, j, hist_sum)
            v_j = max_value(i, j - 1, hist_sum)
            v = min(v_i, v_j)
            cache.update({f"{i}-{j}": v - hist_sum})
            return v

        v_0 = min_value(1, l - 1, nums[0])
        v__1 = min_value(0, l - 2, nums[l - 1])
        return max(v_0, v__1) >= sum(nums) / 2

执行用时: 44~48 ms (74%~54%)
内存消耗: 14 MB

好了很多，但是还是不够。其它细节比如：数组长度为偶数时玩家一必胜。另外还有动态规划视角的解法（TODO）。

阅读材料

• Stuart Russell and Peter Norvig. Artificial Intelligence: A Modern Approach. Prentice Hall. 3rd 2009.
  (Chapter 5: Adversarial Search)

扩展阅读

• ⭐ 浅述：从 Minimax 到 AlphaZero，完全信息博弈之路 - 知乎专栏 (opens new window)